Herkes için Kuantum Elektrodinamiği -2

twitter.com/yazicie

Feynman Diagramları ve Vakum Etkileşmeleri

    20. yüzyılın başlarında geliştirilen kuantum mekaniği, şaşırtıcı sonuçlar doğurmakla birlikte, fotonun ve ışık hızına yakın parçacıkların davranışı hakkında öngörüde bulunamıyordu. Problem, kuantum mekaniği ile Einstein'ın özel izafiyet teorisinin birleştirilmesindeydi.

    "Özel izafiyet teorisi" (relativite) yüksek hızlarda ve ışık hızında hareket eden cisimlerin uzay-zamandaki davranışlarını güzelce tasvir eden bir modeldi. Bu teoriye göre farklı hızlarda hareket eden iki farklı referans sistemi için zaman ve mekan tamamen farklı davranıyordu. Mesela çok hızlı hareket eden bir uzay gemisindeki birine dünyadan baktığımız zaman, uzay gemisindeki zamanın bize göre daha yavaş ilerlediğini görürüz. Uzay gemisinin boyutlarını olduğundan daha kısa görürüz. Dünyadaki iki farklı yerdeki gözlemciler için eşzamanlı gerçekleşen bir olayın, farklı referans sistemlerinden bakıldığında farklı zamanlarda gerçekleştiği görülür.

Kuantum mekaniği ise çok küçük boyutlardaki parçacıkların alışageldiğimiz sağduyumuza aykırı davranışlarını tasvir ediyor, şaşırtıcı sonuçlar doğuruyordu. Bilinen Newton mekaniğinde olduğu gibi maddenin hareketi ve konumu hakkında kesin bilgiler vermek yerine, kuantum mekaniği “olasılıklardan” bahsediyor, bir olayı bir belirsizlik dahilinde tahmin edebileceğimizi, ancak nihai bir kesin sonuca ulaşamayacağımızı söylüyordu. Matematiksel kesinliğin uygulama alanı ve şaşmaz doğrulukların bilimi olan fizik, bir anda istatistiksel hesapların elinde, tahminlerin ve ihtimallerin çocuğu oluvermişti. Fakat doğa bu şekilde işliyordu ve kuantum mekaniğine direnmek yerine onu kabullenip fiziğin tüm alanlarını bu yeni teoriye uyarlamak gerekiyordu.

    20. yüzyıl insanlığa tam bir baş ağrısı hediyesiyle birlikte geliverdi. Fiziğin yeni meydan okuması buydu: elektromanyetik alan teorisi, özel izafiyet teorisi ve kuantum mekaniği teorisinin tek çatı altında toplanması. Tüm bu teorilerin kesişiminde bulunan “yüksek hızla hareket eden relativistik parçacıklar ve foton”un davranışlarını net biçimde ortaya koyacak bir “relativistik kuantum teorisine” ihtiyaç vardı.

    Kuantum teorisi ile relativiteyi ilk formülize eden kişi, İngilizlerin Newton'dan sonra en büyük dahisi olarak kabul edilen Paul Dirac oldu. Elekrtomanyetik alanın kuantizasyonunu, parçacıkların yaratma – yok etme operatörlerini tanımlayarak, harmonik salınıcılarla açıklamıştı. Böylece elektrmanyetik radyasyon ve maddenin etkileşiminin nasıl olduğuna dair sır perdesi aralanmaya başladı.

    Kuantum mekaniği, atomik spektrumları açıklamak için, elektronların bir enerji seviyesinden diğerine geçerken bir foton absorbe ettiğini (veya yaydığını) bir önkabul olarak ele aldı. Dolayısıyla erken dönem kuantum mekaniği madde ile fotonun etkileşimini konu alan bir teoriydi, ancak fotonu tüm yönleriyle tanımlamaya yönelik bir önerisi yoktu.

    Bu problemi aşmak için küçük bir fizikçi grubu, kuantum mekaniğini elektromanyetik alanlara da uygulamak için kolları sıvadı. Born, Heisenberg ve Jordan'ın 1926'da öncülük ettiği bu grubun temel argümanları, elektrik ve manyetik alanın da tıpkı kuantum mekaniksel konum ve momentum gibi matrislerle temsil edilmesi gerekliliğiydi. Dirac, 1927'de yayımladığı “Radyasyon Emisyonu ve Absorbsiyonunun Kuantum Teorisi” adlı çalışmada, kuantum mekaniğinin parçacıkların fiziksel nicelikleri için tarif ettiği süreksiz (kesikli) yapıyı alanlara uygulamanın sistematik bir yöntemini bulmuştu. Harmonik salınıcıların kuantum mekaniksel tasvirini kullanarak, elektromanyetik alanın kuantize edilmesiyle fotonların nasıl göründüğünün teorik bir tarifini yapmıştı. Böylece kuantum alan teorisinin de temelleri atılmış oldu.

    Kuantum alan teorisi, uzayı dolduran elekrik, manyetik alan gibi alanların "kuantize edilmesiyle" parçacıklı yapılarının ortaya çıkmasını ifade eder. Yani bir alan, bir maddeyle etkileşime girerse, o alanın temsil edildiği bir parçacık yaratılır. Mesela, elektromanyetik alan bir objektif ile etkileşime girdiğinde objektifte elektromanyetik alan kendisini foton olarak gösterir. Aynı şey elektron gibi parçacıklarda da geçerlidir. Biz bir elektronu bir levhaya gönderdiğimizde elektron dalga yapısına sahip bir alan gibi davranır. Ama elektron levhaya çarptığında bir parçacık olarak etkileşime girer. Kısacası, alanlar gözlemlendiği (etkileşime girdiği) ana kadar alan, gözlemlendikleri anda ise parçacıktır.

Alan    --->      Kuantize edilen alan      --->      parçacık 

(Uzayı dolduran) ---> (etkileşim süreci) ---> (gözlemlenen)

    Kuantum elektrodinamiği iki sütun üzerine bina edilmişti. Birincisi, elektromanyetik alanın kuantize edilmiş hali olan fotonlarla ilgiliydi. İkincisi ise elektronun relativistik teorisiydi ki bu, Dirac denkleminin bel kemiğini oluşturur zaten.

    Foton ve elektronların etkileşimini matematiksel olarak anlamak için pertürbasyon yöntemleri kullanılır. Pertürbasyon teorisi, tam çözümü olmayan bir problemin, bu probleme benzer başka bir problemden yola çıkarak yaklaşık çözümler elde etmek için matematiksel yöntemler aranmasından ibarettir. Kesin çözümü olan bir probleme, küçük bir terim ekleyerek çözülmek istenen asıl probleme benzer bir yapı elde edilebiliyorsa, pertürbasyon teorisi kullanılabilir.

    Elimizde bir problemin kesin bir çözümü olan K ifadesi olsun. Çözümünü aradığımız problem de P olsun. K'ya küçük parametreler (e_i) ekleyerek aradığımız çözüme yaklaşabileceğimiz durumlar vardır: K kesin çözümüne küçük bir terim ekleyerek K'yı pertürbe ederiz. Daha sonra bu küçük sapmanın miktarı kullanılarak kuvvet serisi terimlerine açarız.

P = K + e₁ K₁ + e₂ K₂ +...

    Genelde eklenen terimler arttıkça, katkıları da o mertebede azalır. Dolayısıyla en büyük katkıyı e₁ terimi sağlar. Diğer yüksek mertebeli terimlerin katkıları giderek küçüldüğü için belli bir noktada ihmal edilirler ve hesaplanmazlar.

    Kuantum elektrodinamiğinin formülasyonunda da pertürbasyon yöntemine başvurmak gerekti. Fakat burada fizikçileri uzun süre meşgul edecek tam bir baş belası problemle karşılaşıldı. Pertürbasyon metoduyla sadece birinci mertebenin çözümü elde edilebiliyordu. Üst mertebeli katkıların matematiksel ifadeleri küçülmek bir yana, sonsuza ıraksayan integraller ile doluydu. Giderek küçülmesi gereken katkılar, sonsuz değerler olarak ortaya çıkıyordu. Fiziksel gerçeklikle hiç de uygun olmayan bu durumun, özel izafiyet ile kuantum mekaniği arasındaki bir uyumsuzluktan doğduğu düşünülerek çözümsüz olarak kaldı.

    Fakat çok geçmeden, bu sonsuz katkı veren integralleri halının altına süpürmenin bir yöntemi bulundu. Renormalizasyon denilen bu yöntemle, sonsuz katkılı terimler, fiziksel değerlerden ayıklanarak doğru hesaplamalar yapılabildi.

    Özetle, kuantum alan teorisinde elektromanyetik alan kuantaları olan, diğer bir deyişle ışık taşıyıcısı parçacıklar olan fotonlar, elektronlar tarafından absorbe edilebiliyor, ve yayımlanabiliyordu. Elektromanyetik alanla etkileşime giren tüm elektrik yüklü parçacıklar foton soğurup foton ışıyabiliyordu. 1930'lara gelindiğinde iki Rus fizikçi o gün için çok sıradışı bir önermede bulundular. Onlara göre sadece fotonlar değil, kütleli parçacıklar da yok olup tekrar var olabilir, birbirleri tarafından soğurulup tekrar yayımlanabilirlerdi. Ambarzumian-Ivanenko hipotezi denilen bu fikir, modern kuantum alan teorisinin ve parçacık fiziğinin temeli oldu.

    Kuantum mekaniğinin izafiyet teorisiyle evliliğinin sonucunda, parçacıkların sürekli birbirlerini yok edip başka parçacıkların açığa çıktığı, birden yok olan, sonra boşlukta tekrar yaratılan parçacık çiftlerinin cirit attığı enteresan bir varlık alemi önümüze serilmişti. Bu yeni sistemde her şey mümkündü ve bu dünyayı açıklamak için kullanılan dil haddinden fazla soyuttu, aşırı matematikseldi. Neler olduğunu anlatmak için sadece ama sadece karmaşık denklemler kullanılıyordu.

    Hesaplamaların zorluğundan ve kendini ifade sıkıntısından bunalan bu yeni teoriye sıradışı bir genç el atıverdi. Richard Feynman isimli bu genç, o güne kadar kuantum mekaniğinde hayal bile edilmemiş olan, problemleri görselleştirmenin ve en karmaşık süreçleri basit şekillerle ifade etmenin bir yolunu bulmuştu. Mottosu, “bir şeyin gerçekleşme ihtimali varsa, gerçekleşir” sözü oldu. Gerçekten de kuantum mekaniği bize bundan başka bir şey söylemiyordu. Mesela, bir parçacığın iki nokta arasında gittiği yolu hesaplamak istiyorsak, o iki nokta arasındaki mümkün olan tüm muhtemel yolları hesaba katmak zorundaydık. Bir parçacığın konumunu belirlemek istiyorsak, uzaydaki her noktayı hesaba dahil etmek zorundaydık.

    Feynman da etkileşime hangi parçacıkların girdiğini ve etkileşim sonucunda hangi parçacıkların çıktığını temel aldı. Bu süreçte mümkün olan tüm ara etkileşimleri hesaba kattı. Böylece o parçacıkların birbirleriyle etkileşim şiddetlerini, etkileşim sürelerini, kütlelerini, ne ihtimalle o etkileşime gireceklerini vs. her türlü ölçülebilir fiziksel değeri hesaplamanın yoluna ışık tuttu. 

    Her etkileşimi Feynman Diagramı denilen bir şekille ifade ediyor, şekildeki her bir basamağa karşılık gelen matematiksel bir ifade yazıyordu. Böylece her bir süreci temsil eden şekil, ayrı bir matematiksel denklemle temsil ediliyordu. Sonuçta tüm muhtemel etkileşimleri sembolize eden şekillerin, fiziksel katkılarını matematiksel olarak hesaplayabiliyordu.

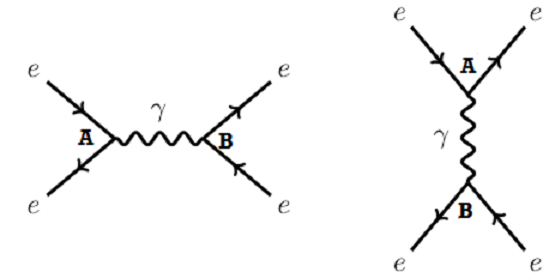
    Yukarıdaki Feynman diyagramlarında solda, bir elektron ve bir antielektronun birbirlerini yok etmesi sonucu bir foton açığa çıktığı, daha sonra bu fotondan tekrar bir elektron - antielektron çifti yaratıldığı gösterilir. Sağda ise bir elektron ile bir antielektron arasında bir foton alış-verişi gerçekleştiği gösterilir. Aslında tamamen farklı gerçekleşen bu iki süreç, neticesi itibariyle aynı fiziksel sonucu verir: bir elektron ile bir antielektron elektromanyetik kuvvet sonucu birbirleriyle etkileşime girip saçılmışlardır. Bu etkileşimin şiddetini hesaplamak için her iki Feynman diyagramının katkısını da göz önünde bulundurmak gereklidir. "Gerçekte hangi süreç oldu?" sorusunun cevabı, "her ikisi de" şeklindedir. Kuantum mekaniğinin acayipliği de işte burada. Üstelik aynı fiziksel sonucu veren sonsuz sayıda Feynman diyagramı çizmek de mümkün.

    Yukarıdaki şekilde yine aynı fiziksel süreç temsil ediliyor. Fakat burada foton alış-verişi esnasında foton vakumla etkileşime girerek bir parçacık çiftine bozunuyor, sonra bu parçacık çifti tekrar yok olup yeni bir foton yaratılıyor. Bu süreç önceki süreçlere nisbeten daha karmaşık olduğu için gerçekleşme ihtimali daha düşük, dolayısıyla fiziksel sürece katkısı da daha küçük oluyor. Feynman diyagramları karmaşıklaştıkça hesaplamaları daha zor, fiziksel katkıları da daha az oluyor.

    KED teorisi yapılan deneylerle sürekli test ediliyor, daha üst mertebeli katkılar da hesap edilerek yeni teorik hesaplar yapılıyor. Günümüzde KED öyle sağlam sonuçlar veriyor ki, yapılan deneylerle teori, sıfırdan sonra onuncu mertebelere kadar kesinlikte uyum içerisindedir.

    KED'nin başarısından güç olan teorik fizikçiler, aynı matematiksel alt yapıyı kullanarak nükleer reaksiyonlardan sorumlu olan zayıf etkileşimi de açıkladılar. Hatta 1960'lara gelindiğinde elektromanyetik etkileşim ile zayıf etkileşimin aslında aynı kuvvetin yansımaları oldukları anlaşıldı. Elektrik, manyetizma ve nükleer reaksiyonlar tek bir çatı altında toplanarak birleştirimiş oldular.

    Fizikçiler aynı matematiksel alt yapıyla, proton ve nötronları bir arada tutan güçlü etkileşimin de teorisini geliştirdiler. "Kuantum renk dinamiği" denilen bu yeni teoriyle doğada gözlemlenen 4 temel kuvvetin 3'ü sağlam bir matematiksel izaha kavuşmuş oldu. KED'in öncülük ettiği doğanın bu matematiksel resmine "Standard Model" ismi verilir.

    Şimdi yeni hedef, güçlü etkileşimin de, elektrozayıf etkileşim ile aynı kökten geldiğini gösterebilmek ve böylece tüm kuvvetlerin birleştirildiği büyük bir birleşik kuram elde etmek. Bir sonraki adım ise bu çatıdan şimdilik çok uzak görünen kütleçekim kuvvetinin de diğer kuvvetlerle irtibatlı olduğunu ispatlayarak "herşeyin teorisini" elde etmektir.

http://plato.stanford.edu/entries/quantum-field-theory/qft-history.html
http://en.wikipedia.org/wiki/History_of_quantum_field_theory
http://en.wikipedia.org/wiki/History_of_electromagnetic_theory